由于毕业课题涉及到绘制复合物相互作用能的势能面,所以我为了绘制得到较美观的势能面等高线图而仔细看了matplotlib的contourf函数的手册。
实际上一开始是想用gnuplot画图的,但我需要绘制的势能面有一个挺麻烦的特征:其数值的范围非常大。也就是在两个分子靠得比较近的较小的区域里,相互作用能的数值大约为几万(正值,是一种互相排斥的状态);而在两个分子远离的较大区域内,此时作用很弱,因此数值接近零。这种情况下,gnuplot在没有其他设置(我不太清楚是否真的有相关的选项)的情况下绘制出的图效果很不好。
后来就想着试试用Origin绘图。一开始其实很快就绘制好了,而且Origin允许手动选择特定数值的等高线以及设置填色。但是画完后还是发现不够完美,这是因为等值线的数值label是无法自定义的。因此图上的label非常的混乱,相互重叠并且分布很难看。
之后就尝试使用matplotlib绘图了,虽然以前并没有用过。一开始绘制出的和gnuplot的一样,但在仔细研究了手册后,发现选项相当多。因此我认为matplotlib的灵活度非常适合绘制我所需的图形。
这篇文章里,我将适当介绍下与绘制等高线图相关的几个很重要的选项。因为我的毕业论文并没有写完,所以就不用自己的数据作为例子。这里首先用函数
作为例子。
该函数的三维图形如下图。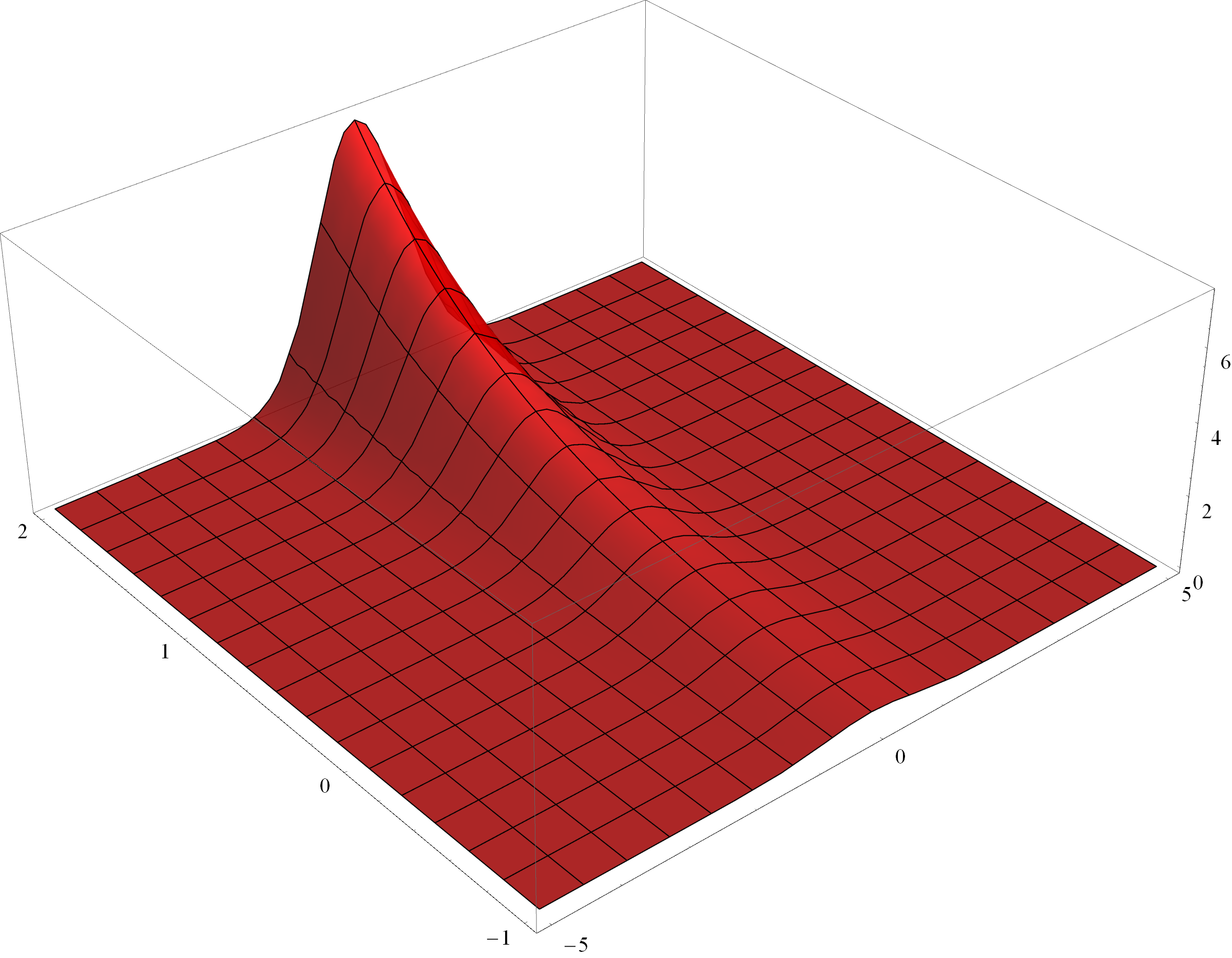
由于指数函数的增长很快,其最大值会很容易远大于零。
接下来画等高线(填色)图。
首先只绘制等高线并进行填色。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15import numpy as np
import matplotlib.pyplot as plt
def f(x,y):
return np.exp(-x**2)*np.exp(y)
fig, ax = plt.subplots()
ax.set_xlabel('x', fontsize=16)
ax.set_ylabel('y', fontsize=16)
n = 200
x = np.linspace(-2,2,n)
y = np.linspace(-2,2,n)
X,Y = np.meshgrid(x, y)
plt.contourf(X, Y, f(X, Y), levels=10, alpha=.75, cmap='coolwarm')
C = plt.contour(X, Y, f(X, Y), levels=10, colors='black', linewidth=.5)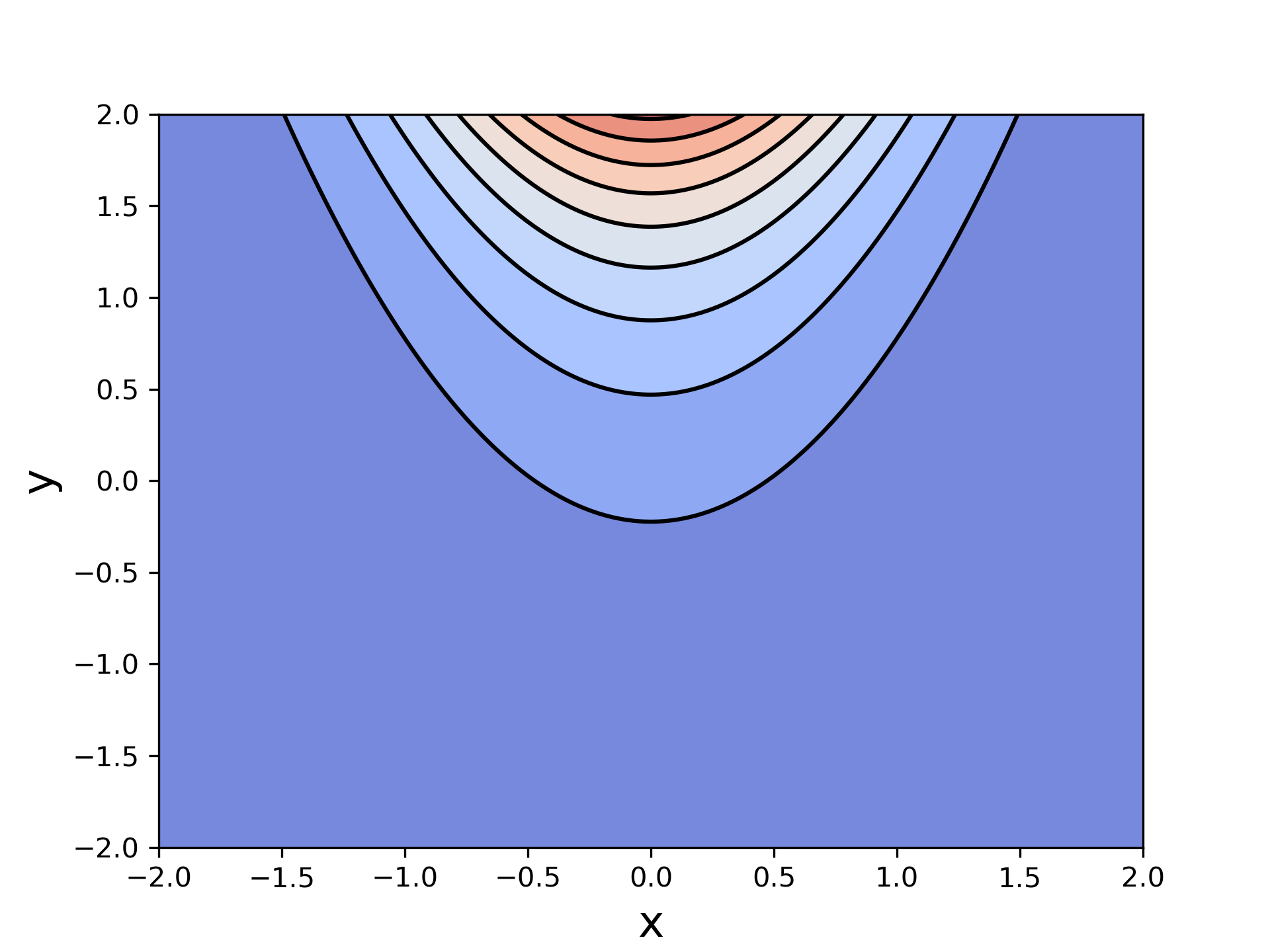
这里就涉及到一个非常重要的选项levels,在上面的例子中我们令其为整数10,意味着将图像分为10个区域。顺便提一下,倒数第二行代码contourf是负责填色的,最后一行的contour是绘制等高线的。如果不需要填色,倒数第二行代码可以去掉。反之也可以。
要在等值线上加上label注明其数值,可用clabel实现。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16import numpy as np
import matplotlib.pyplot as plt
def f(x,y):
return np.exp(-x**2)*np.exp(y)
fig, ax = plt.subplots()
ax.set_xlabel('x', fontsize=16)
ax.set_ylabel('y', fontsize=16)
n = 200
x = np.linspace(-2,2,n)
y = np.linspace(-2,2,n)
X,Y = np.meshgrid(x, y)
plt.contourf(X, Y, f(X, Y), levels=10, alpha=.75, cmap='coolwarm')
C = plt.contour(X, Y, f(X, Y), levels=10, colors='black', linewidth=.5)
plt.clabel(C, inline=True, fontsize=10)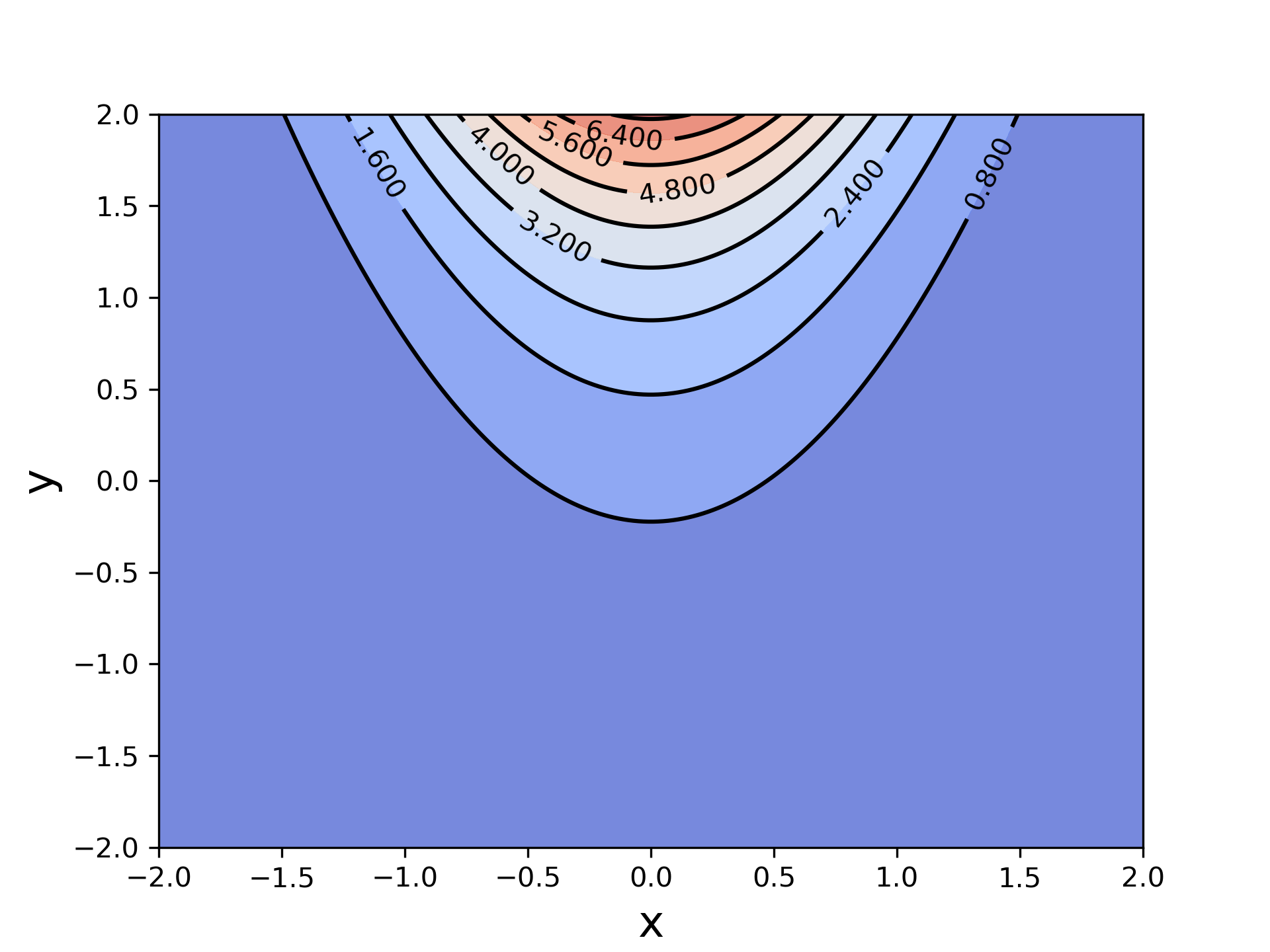
自动标记的label有一些重叠,之后将会演示手动选择label的位置。
以上的图形中,下部分没有等高线的分布。为了让整个图形更为平衡,我们手动控制范围的划分。
1 | import numpy as np |
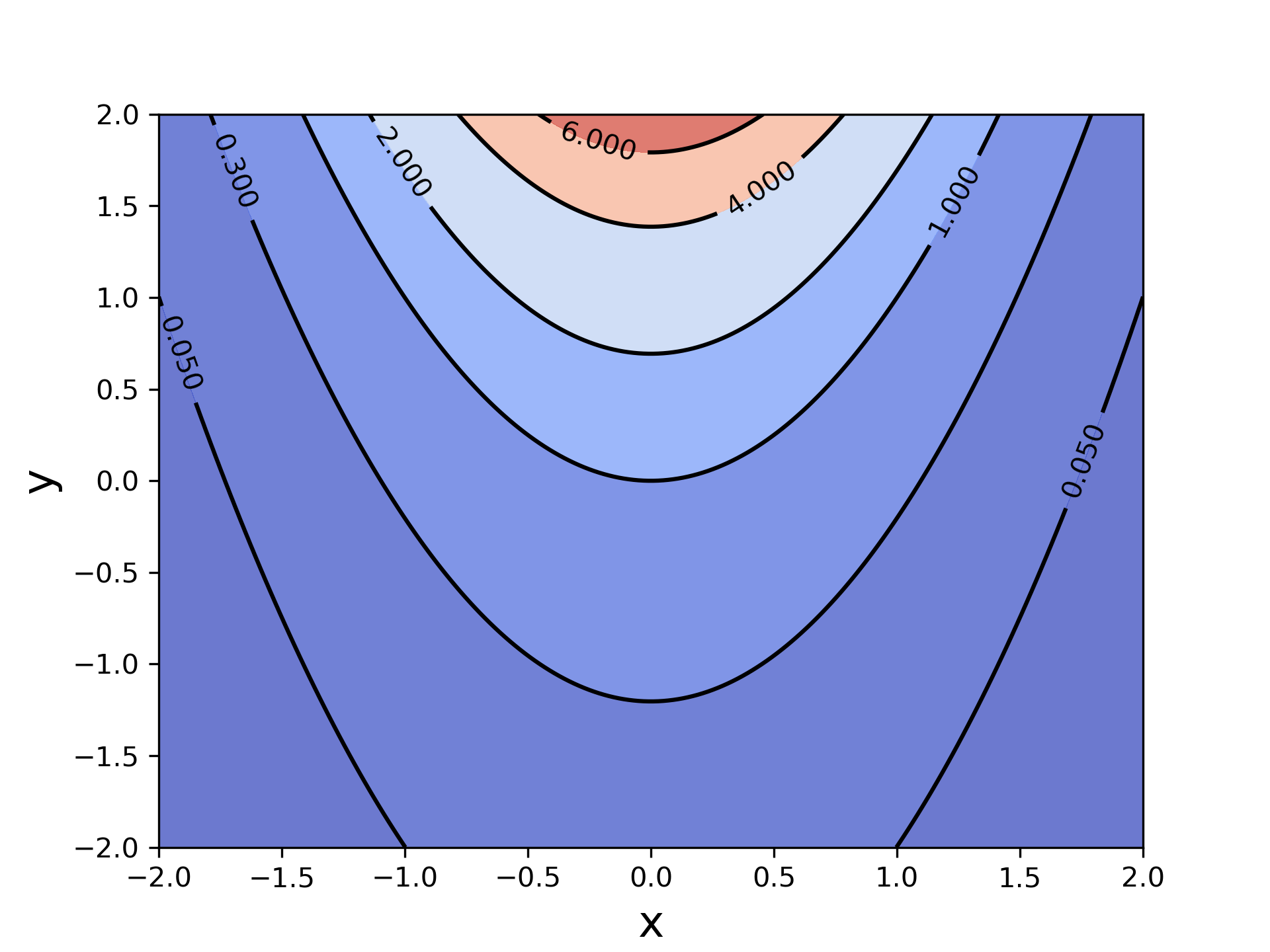
在这个例子中,我们给contourf和contour手动选择了其区域。对于contour,我们令其在函数值分别为 (0.05,0.3,1,2,4,6) 的等值线进行划分。对于contour,虽然本质上其划分方式一样,但这里还是要额外在两端加上最小值和最大值。因为填色本质上是对一个区间内填色,如果其设置和contour完全一样,在包含最小值和最大值的区域中是没有填色的。可以亲自验证一下。
接下来则是介绍自定义label的位置。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20import numpy as np
import matplotlib.pyplot as plt
def f(x,y):
return np.exp(-x**2)*np.exp(y)
fig, ax = plt.subplots()
ax.set_xlabel('x', fontsize=16)
ax.set_ylabel('y', fontsize=16)
n = 200
x = np.linspace(-2,2,n)
y = np.linspace(-2,2,n)
X,Y = np.meshgrid(x, y)
line_lv = [0.05,0.3,1,2,4,6]
cf_lv = [0,0.05,0.3,1,2,4,6,np.exp(2)]
lb_pos = [(0,1.8),(0,1.4),(0,0.8),(-0.75,0.7),(0.75,0.7),\
(-1,0),(1,0),(-1.5,-1),(1.5,-1)]
plt.contourf(X, Y, f(X, Y), levels=cf_lv, alpha=.75, cmap='coolwarm')
C = plt.contour(X, Y, f(X, Y), levels=line_lv, colors='black', linewidth=.5)
plt.clabel(C, inline=True, fontsize=10, manual=lb_pos)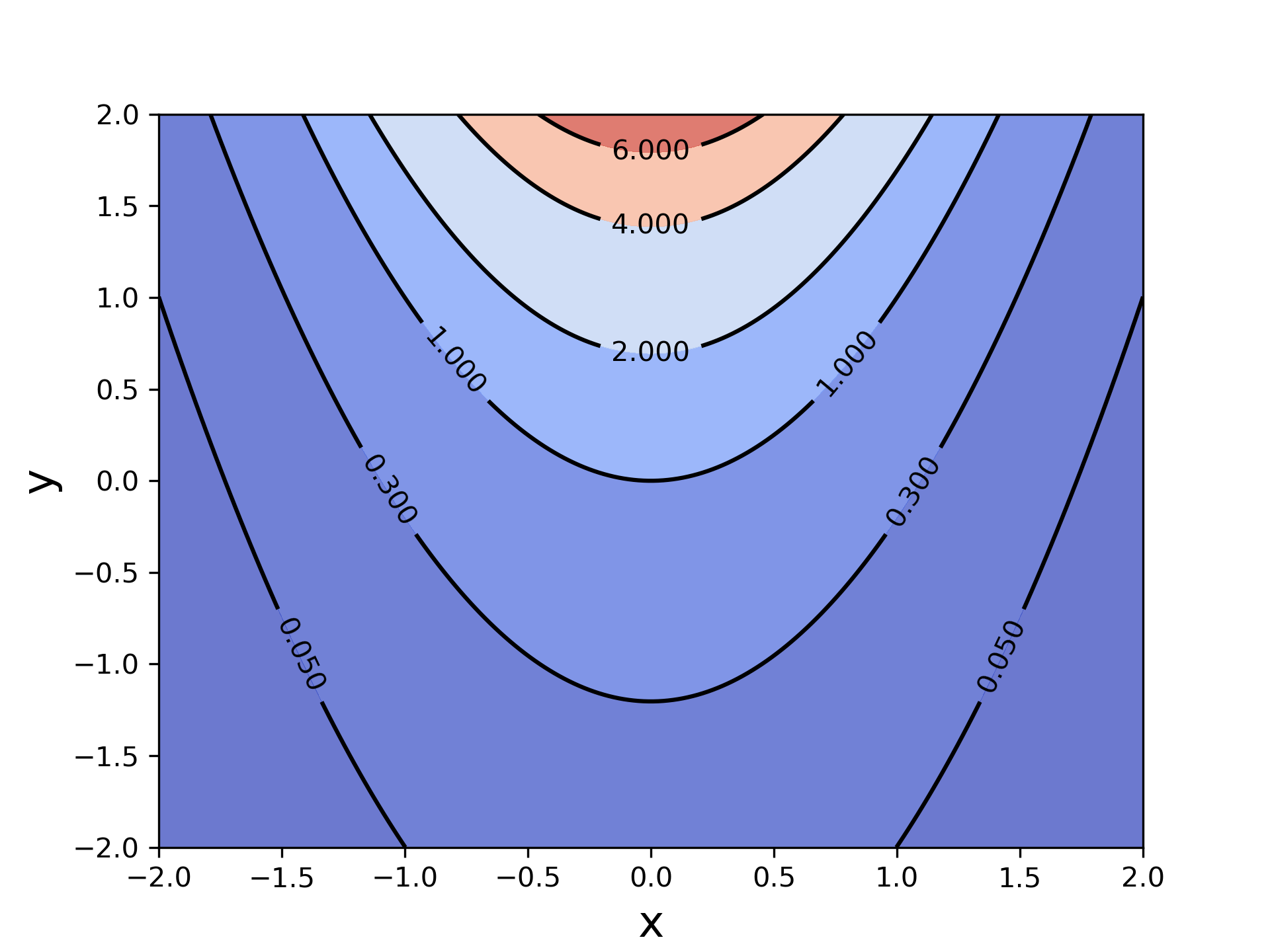
clabel提供了一个选项manual,虽然其输入数据中包含一组坐标,但严格来讲它并不是说就会在那些点上显示label。假定已经有了包含等高线的图,但还没有设定label,我们在等值线想要显示label的位置“点击”一下,然后程序就会在这点附近的等值线上显示其数值(假如这里的等高线较密,有可能会标记到你不需要的线上,需要慢慢调整)。实际上matplotlib真的可以通过这种交互式的方式设定label位置,但我之前测试的时候好像没有成功。具体可以参考手册的相应内容。点的数量与等高线的数量无关,单纯只是看你想标多少个。
最后讲讲当数值范围非常大的时候,如何保证填色具有很好的区分度。我们将前面的函数稍微调整一下:
此时函数值的范围比之前更大。
我们首先只控制等值线的数值1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17import numpy as np
import matplotlib.pyplot as plt
def f(x,y):
return np.exp(-x**2)*np.exp(3*y)
fig, ax = plt.subplots()
ax.set_xlabel('x', fontsize=16)
ax.set_ylabel('y', fontsize=16)
n = 400
x = np.linspace(-2,2,n)
y = np.linspace(-2,2,n)
X,Y = np.meshgrid(x, y)
line_lv = [0.005,0.1,1,10,90,300]
cf_lv = [0,0.005,0.1,1,10,90,300,np.exp(6)]
plt.contourf(X, Y, f(X, Y), levels=cf_lv, alpha=.75, cmap='coolwarm')
C = plt.contour(X, Y, f(X, Y), levels=line_lv, colors='black', linewidth=.5)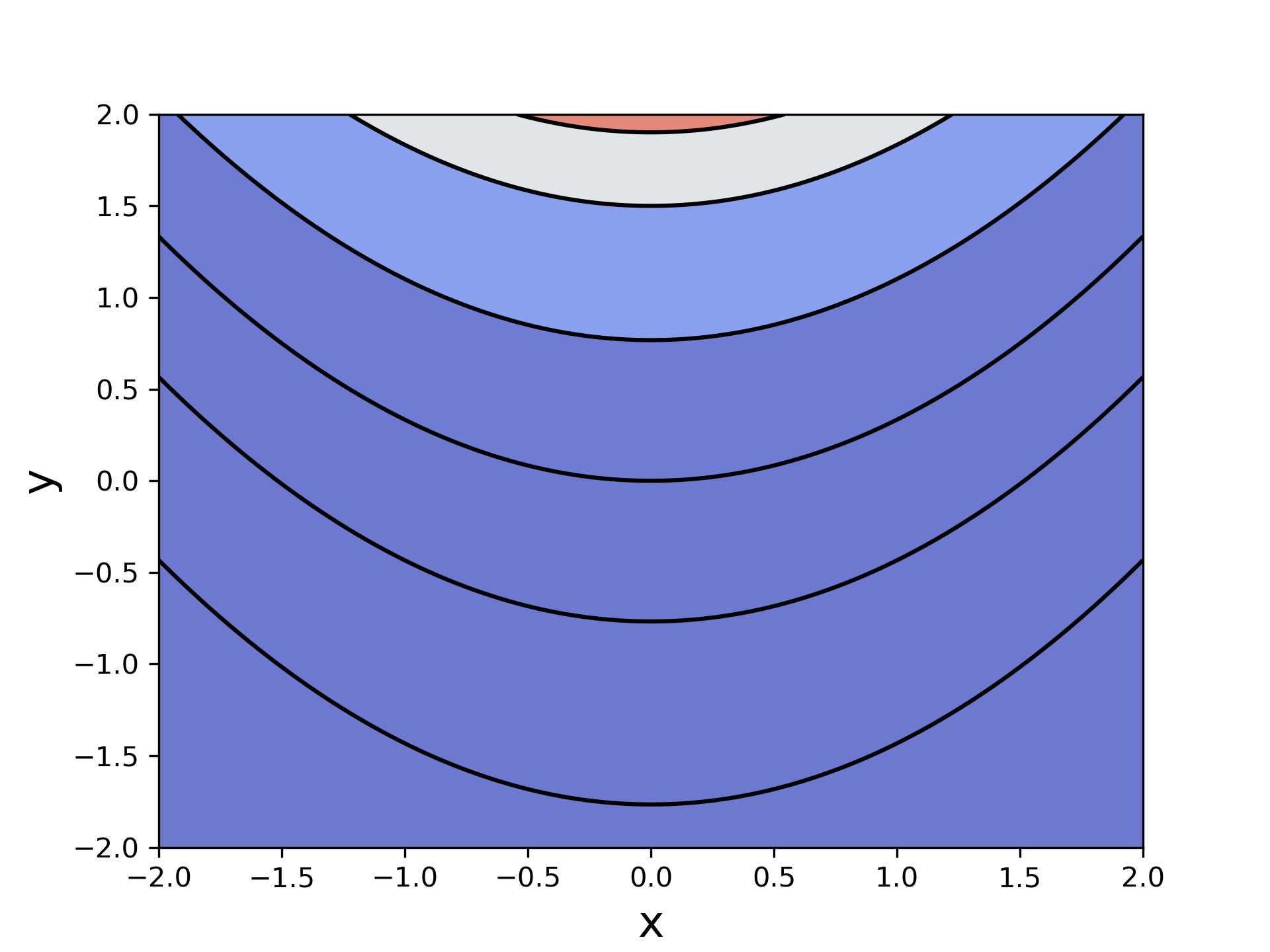
可以看到,此时较平坦的部分的颜色几乎毫无区分度。
我们使用norm选项对颜色的归一化进行调整。1
2
3
4
5
6
7
8
9
10
11fig, ax = plt.subplots()
ax.set_xlabel('x', fontsize=16)
ax.set_ylabel('y', fontsize=16)
n = 400
x = np.linspace(-2,2,n)
y = np.linspace(-2,2,n)
X,Y = np.meshgrid(x, y)
line_lv = [0.005,0.1,1,10,90,300]
cf_lv = [0,0.005,0.1,1,10,90,300,np.exp(6)]
plt.contourf(X, Y, f(X, Y), levels=cf_lv, alpha=.75, norm=colors.PowerNorm(gamma=0.2), cmap='coolwarm')
C = plt.contour(X, Y, f(X, Y), levels=line_lv, colors='black', linewidth=.5)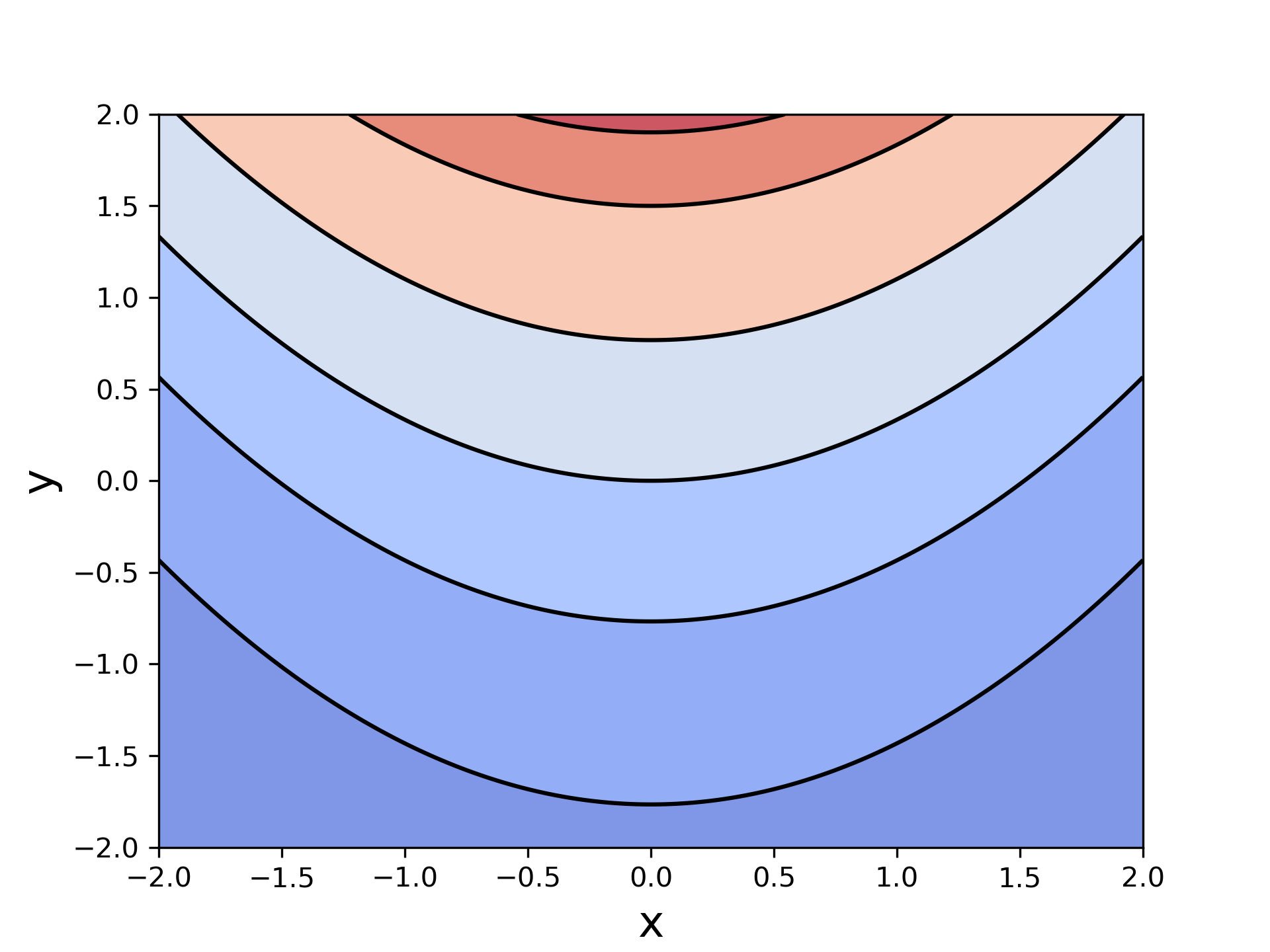
可以看到,这下颜色区分度就很好。
归一化的方式有很多,这里用的是基于幂函数 (y=x^\gamma) 的,gamma的取值需要自行调整。其他算法可在手册中找到。