Scarlet Land

0%

利用.fch文件计算电子密度的代码

发表于 更新于 分类于

最近在看密度泛函的书，于是就想自己写一个能计算电子密度的程序，这样就可以具体地了解一些体系。而且由于更早一些时候才正经学了基组的知识，想弄清楚怎么把市面上的基组放在程序中使用（之前写HF程序用的是STO-3G，不涉及到分裂价层，而且没有涉及更多的壳层）。所以写这么一个程序还是可以帮我学到很多东西的。

代码上传到GitHub：https://github.com/St-Maxwell/ElectronDensity

参考了Sobereva的文章：高斯fch文件与wfn波函数文件的介绍及转换方法、利用wfn文件计算电子密度的代码的编写方法。

电子密度

在空间$\mathbf{r}$处找到任意一个电子的概率。 $$ \rho(\mathbf{r}) = N \int |\Psi(\mathbf{x}_1, \mathbf{x}_2,\ldots,\mathbf{x}_N)|^2\, d\omega_1 d\mathbf{x}_2\ldots d\mathbf{x}_N $$ 将上式展开为空间轨道（分子轨道）$\{\psi_a\}$，为 $$ \rho(\mathbf{r}) = 2 \sum\limits_a^{N/2} |\psi_a(\mathbf{r})|^2 $$ 若是自然轨道，则为 $$ \rho(\mathbf{r}) = \sum\limits_a^{N/2} \lambda_a |\eta_a(\mathbf{r})|^2 $$ 其中$\eta_a$是自然轨道，$\lambda$是自然轨道占据数。 实际计算中将用一组基函数将轨道展开，则密度的表达式可写为 $$ \rho(\mathbf{r}) = \sum\limits_a^{N/2} \lambda_a \left| \sum\limits_i C_{ai} \varphi_i(\mathbf{r}) \right|^2 $$ $C_{ai}$是展开系数，$\lambda_a$对于分子轨道就是$2$，对于自然轨道则是非整数。 基函数同样可以用一组Gaussian型函数（Gaussian Type Function，GTF）展开: $$ \varphi = \sum\limits_i a_i \chi_i^\text{GTF}(x,y,z) $$ $a_i$是收缩系数，$\chi^\text{GTF}$假定是Cartesian型GTF，有如下形式 $$ \chi = N x^{l_x} y^{l_y} z^{l_z} \mathrm{e}^{-\zeta r^2} $$ 归一化系数$N$的表达式为 $$ \begin{aligned} N &= \left( \frac{2\zeta}{\pi} \right)^{3/4} \left[ \frac{(4\zeta)^{l_x+l_y+l_z}}{(2l_x-1)!!(2l_y-1)!!(2l_z-1)!!} \right]^{1/2} \\ &= \left( \frac{2\zeta}{\pi} \right)^{3/4} \left[ \frac{(8\zeta)^{l_x+l_y+l_z}l_x!l_y!l_z!}{(2l_x)!(2l_y)!(2l_z)!} \right]^{1/2} \end{aligned} $$

电子密度的梯度

电子密度的梯度为 $$ \nabla \rho(\mathbf{r}) = \frac{\partial \rho(\mathbf{r})}{\partial x}\mathbf{x} + \frac{\partial \rho(\mathbf{r})}{\partial y}\mathbf{y} + \frac{\partial \rho(\mathbf{r})}{\partial z}\mathbf{z} $$ 以$\partial \rho/\partial x$为例： $$ \begin{aligned} \frac{\partial \rho}{\partial x} &= \frac{\partial}{\partial x} \sum\limits_a^{N/2} \lambda_a \psi_a^2(\mathbf{r}) \\ &= \sum\limits_a^{N/2} 2\lambda_a \psi_a(\mathbf{r}) \frac{\partial \psi_a(\mathbf{r})}{\partial x} \end{aligned} $$ 分子轨道的导数最终可以用GTF的导数的线性组合表示： $$ \frac{\partial \psi_a(\mathbf{r})}{\partial x} = \sum\limits_i C_{ai} \sum\limits_j a_{ij} \frac{\partial \chi_j(\mathbf{r})}{\partial x} $$ GTF关于$x$的导数很容易得到，为 $$ \frac{\partial \chi_j(\mathbf{r})}{\partial x} = (l_x x^{l_x-1} - 2\zeta x^{l_x+1}) N y^{l_y} z^{l_z} \mathrm{e}^{-\zeta r^2} $$ 梯度的模 $$ |\nabla \rho| = \sqrt{\bigg(\frac{\partial \rho}{\partial x}\bigg)^2 + \bigg(\frac{\partial \rho}{\partial y}\bigg)^2 + \bigg(\frac{\partial \rho}{\partial z}\bigg)^2} $$

需要从.fch文件读取的量

波函数类型 如果是自然轨道，需要手动将.fch文件第一行内容改为isNO； 从第二行确定波函数为R、U、RO。若使用的方法首字母为O，且为闭壳层的情况，会误认为波函数为RO，虽然并不影响密度的计算。 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
SP        RB3LYP                                   6-31G(d,p)
电子数
Number of electrons                        I               10
Number of alpha electrons                  I                5
Number of beta electrons                   I                5
基函数数目
Number of basis functions                  I               25
收缩壳层数目
Number of contracted shells                I               10
原函数数目
Number of primitive shells                 I               21
壳层类型
Shell types                                I   N=          10
每个壳层的收缩度
Number of primitives per shell             I   N=          10
原函数的指数
Primitive exponents                        R   N=          21
原函数收缩系数
Contraction coefficients                   R   N=          21
原函数收缩系数（sp(p)型函数）
P(S=P) Contraction coefficients            R   N=          21
基函数坐标
Coordinates of each shell                  R   N=          30
分子轨道系数
Alpha MO coefficients                      R   N=         625
对于自然轨道，这一部分数据实际上是轨道占据数
Alpha Orbital Energies                     R   N=          25

.fch文件波函数类型

Gaussian

  • 限制性分子轨道
    • 闭壳层：默认即可
    • 限制性开壳层：RO
  • 非限制性分子轨道
    • 开壳层：默认即可
    • 自旋极化单重态：UHF/DFT guess=mix
  • 自然轨道
    • density=current + guess(save,only,naturalorbitals) chkbasis
    • 限制性闭壳层：默认
    • 非限制性开壳层：默认
    • 限制性开壳层：不支持（RO后HF都没有解析梯度）
    • 自旋极化单重态：以UHF/DFT guess=mix作为参考态
    • Gaussian输出的.fch中，自然轨道不包含自旋信息，其占据数为$0 \text{--} 2$。虽然会输出beta轨道信息，但实际上和alpha轨道的信息一模一样。

用法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
use m_basis_func
use m_routines
type(molecule) :: mol
integer :: iounit
character(len=80) filename
real(kind=8) :: x, y, z

! read .fch file
write(*,*) "Input .fch file"
read(*,*) filename
open(newunit=iounit, file=filename, status='old', action='read')
call read_basis_func(iounit, mol)
call read_mo_coeff(iounit, mol)
close(iounit)

write(*,*) mol%density(x, y, z, 't')
! 't' - total density
! 'a' - alpha density
! 'b' - beta density
write(*,*) mol%den_grad(x, y, z, 'x')
! 'x' - x component of gradient
! 'y' - y component of gradient
! 'z' - z component of gradient
! 'm' - magnitude of gradient

例子

$\text{CH}_3$自由基



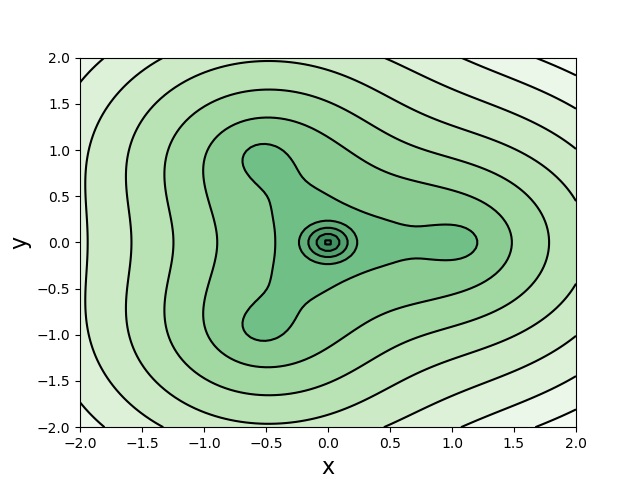
自由基所在平面上的电子密度。

$\text{H}_2$分子



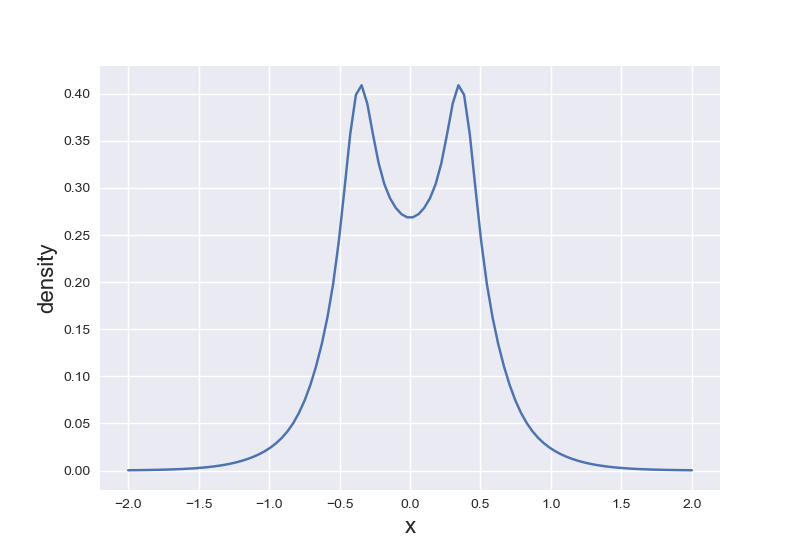
$\text{H}_2$沿所在轴的电子密度，注意到在核的位置电子密度梯度不连续。


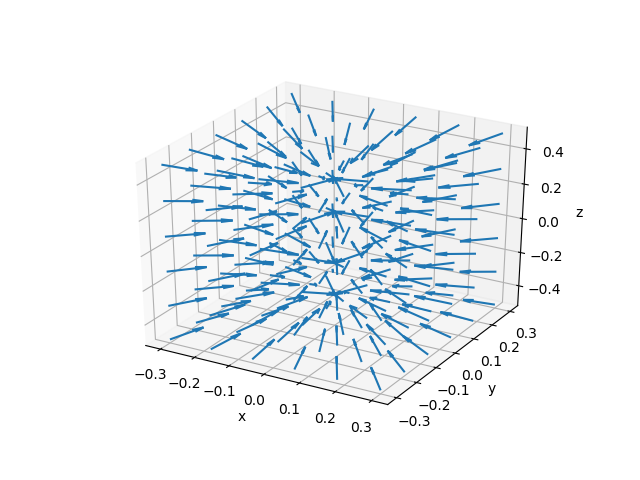
电子密度梯度的空间分布，分子所在轴为$z$轴。可以与上图电子密度的变化进行对照。