氢原子径向波函数数值求解

在此之前，我已经写了一段数值求解一维量子谐振子波函数的Python代码。建议先从该帖子开始阅读（Numerov方法数值求解一维量子谐振子波函数），涉及到的Numerov方法的原理就不再重复了。

首先写出径向部分的Schroedinger方程：

$$-\frac{\hbar^2}{2m} \left( R^{\prime\prime} + \frac{2}{r} R^\prime \right)+\frac{l(l+1)\hbar^2}{2mr^2} R+V(r)R=ER$$

由于Numerov方法处理的是形如$\psi^{\prime\prime}=G(r)\psi(r)$的微分方程，但上式中存在$R^\prime$项，所以需要消掉。

令$F(r)=rR(r)$，所以：

$$R(r)=r^{-1}F(r)$$ $$R^\prime=-r^{-2}F+r^{-1}F^\prime,\ R^{\prime\prime}=2r^{-3}F-2r^{-2}F^\prime$$

代入到径向Schroedinger方程中：

$$-\frac{\hbar^2}{2m} F^{\prime\prime}(r)+ \left[ V(r)+\frac{l(l+1)\hbar^2}{2mr^2} \right]F(r)=EF(r)$$ $$F^{\prime\prime}(r)=G(r)F(r),\ G(r)=\frac{m}{\hbar^2} \left(2V-2E \right)+\frac{l(l+1)}{r^2}$$

递推关系已得到，现在需要讨论边值条件。由于$r\rightarrow 0$时，$R(r)\sim r^l,\ l=0,1,2,\ldots,n$，因此$F=rR$在$r=0$处必为0。

但是这里有一个小问题，$r=0$时，前式中$G(r)$会遇到除以0的情况。为了避免这一情况，我们以一个非常小的$r$作为近似零点（比如令$r=10^{-15}$）。（但是又会带来另一个问题，对于$l=0$的径向波函数，$R(r)|_{r=0}$本应为一非零正值。但我们用该方法产生的结果是在（近似）零点处，波函数为0。然而目前暂时不知道如何处理）

在使用程序实现之前，还是先完成公式的非量纲化。（具体步骤不写了）

$$V_\text{r} =-\frac{e^2}{4\pi\epsilon_0 r}=-\frac{e^{\prime 2}}{r_\text{r}}$$ $$E_\text{r} =\frac{E}{\mu e^{\prime 4} \hbar^{-2}}=-\frac{e^{\prime 2}}{2n^2}$$

得到约化的Schroedinger方程和递推项分别为：

$$F^{\prime\prime}_\text{r}=G_\text{r}F_\text{r},\ G_\text{r}=\frac{l(l+1)}{r_\text{r}^2}-\frac{2}{r_\text{r}}-2E_\text{r}$$

现在就可以使用程序实现了（和之前那个区别不大）。

写的Python代码如下：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

R={"r0":1e-15}
F={"f0":0.0}
G={"g0":0.0}
nn=0
 
l=float(input("Enter angular quantum number(l>=0):"))
s=float(input("Enter the increment sr:"))
m=int(input("Enter the number of intervals m:"))
E=float(input("Enter the reduced energy Er:"))
 
F["f1"]=0.0001
R["r1"]=R["r0"]+s
G["g0"]=l*(l+1)/(R["r0"]**2)-2/R["r0"]-2*E
G["g1"]=l*(l+1)/(R["r1"]**2)-2/R["r1"]-2*E
ss=s*s/12
 
for i in range(1,m+1):
  R["r%s" % (i+1)]=R["r%s" % i]+s
  G["g%s" % (i+1)]=l*(l+1)/(R["r%s" % (i+1)]**2)-2/R["r%s" % (i+1)]-2*E
  F["f%s" % (i+1)]=(-F["f%s" % (i-1)]+2*F["f%s" % i]+10*G["g%s" % i]*F["f%s" \
   % i]*ss + G["g%s" % (i-1)]*F["f%s" % (i-1)]*ss)/(1-G["g%s" % (i+1)]*ss)
  if (F["f%s" % i]*F["f%s" % (i+1)]<0):
    nn=nn+1
 
print("Er="+str(E))
print("Nodes="+str(nn))
for i in range(m+1):
  print("%f %f" % (R["r%s" % i],(F["f%s" % i]/R["r%s" % i])))

运行该程序需要我们输入角量子数、间隔长度、间隔数和能量。

例如，我们想绘制4p轨道径向部分波函数的图像。首先估计能量：$E\text{r}=-\frac{1}{2\times 4^2}=-0.03125$。然后由$-0.03125=-\frac{1}{r_\text{r}}$得到$r=32$。稍取更远的点$r=36$来验证波函数在此处是否趋于0。设间隔长度为0.1，间隔数自然为360。得到结果如下

Er=-0.03125
Nodes=2
0.000000 0.000000
0.100000 0.001000
0.200000 0.001811
0.300000 0.002567
0.400000 0.003247
0.500000 0.003852
0.600000 0.004385
0.700000 0.004853
0.800000 0.005258
0.900000 0.005605
1.000000 0.005899
1.100000 0.006143
...

用以上数据绘图，可看到与解析解得到的结果非常接近。（注：程序输出的数值与波函数的表达式算出的结果并不一定相同，这是因为没有对数值计算得到的结果进行归一化，将其乘以适当的系数后与理论值基本一致。）

之前提到了，对于s轨道，该程序有一些缺陷，由下图可以看出：

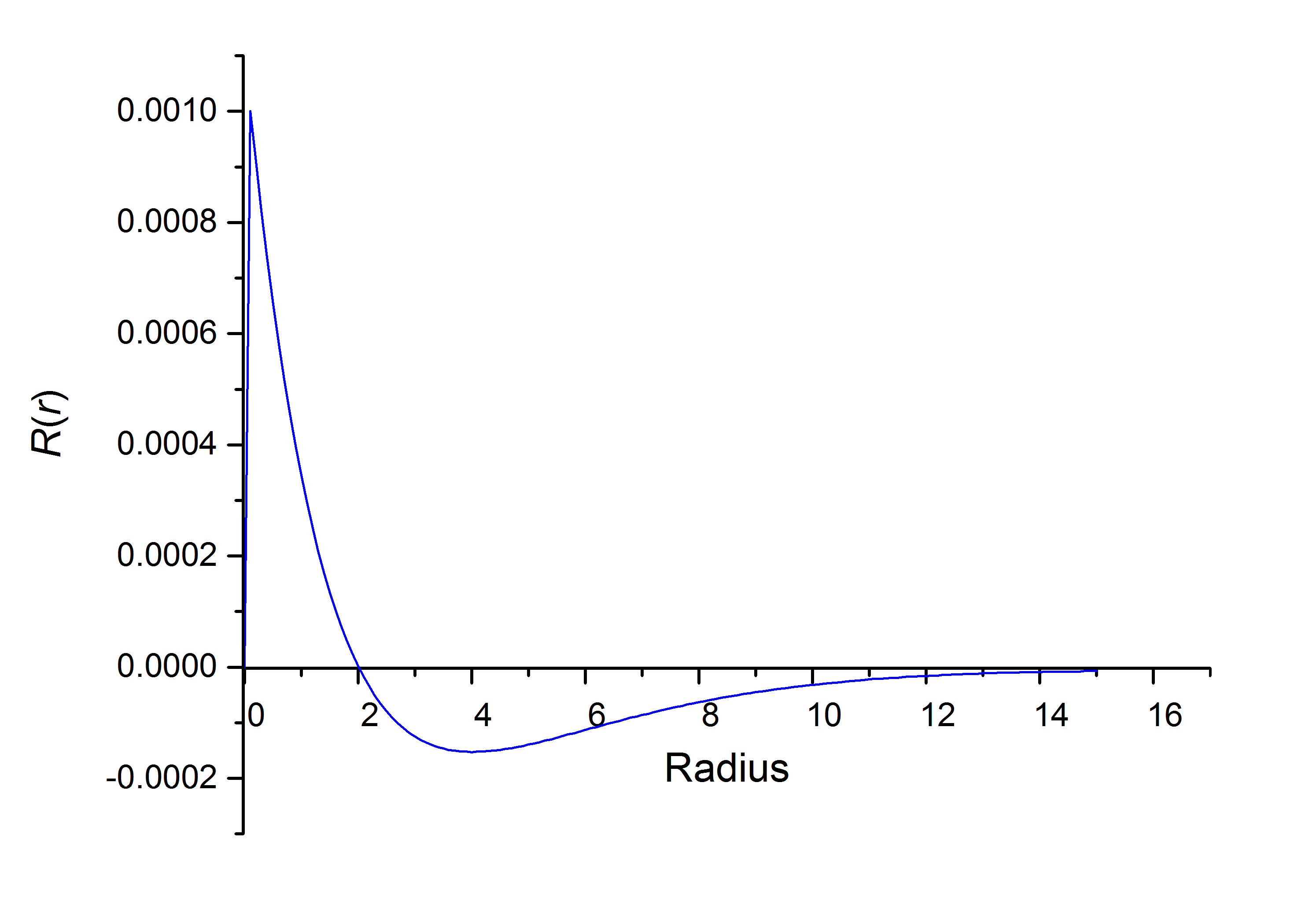
当$r=0$时，$R(r)$本不为0，所以上图在零点附近的表现不太正确（后面是比较吻合的）。